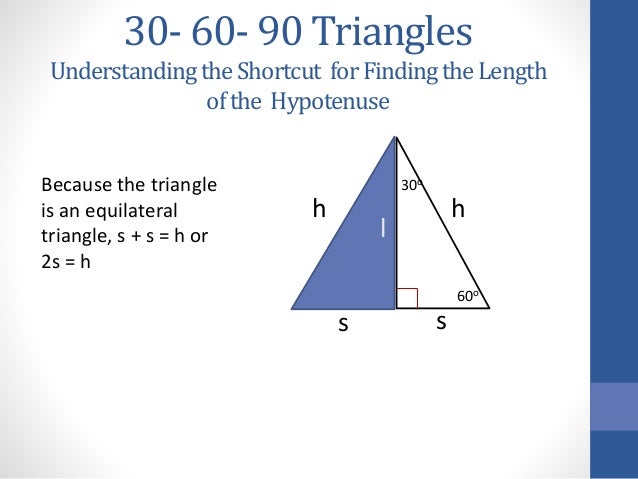
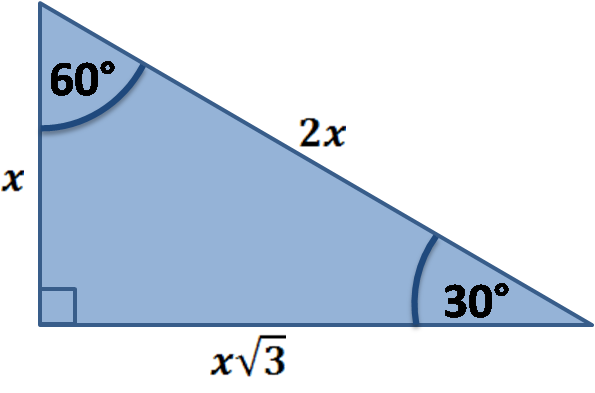
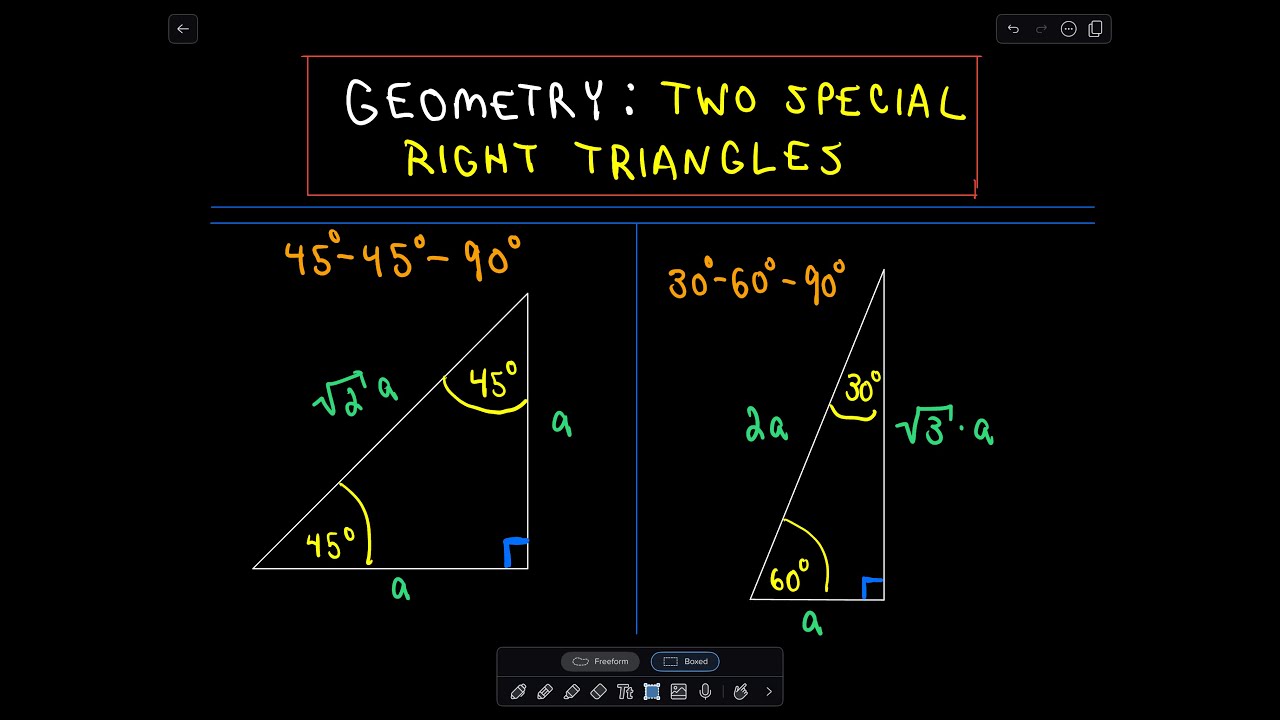
THE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that belowThe measures of its angles are 30 degrees, 60 degrees, and 90 degrees And what we're going to prove in this video, and this tends to be a very useful result, at least for a lot of what you see in a geometry class and then later on in trigonometry class, is the ratios between the sides of a triangleNow when we are done with the right triangle and other special right triangles, it is time to go through the last special triangle, which is 30°60°90° triangle It also carries equal importance to 45°45°90° triangle due to the relationship of its side It has two acute angles and one right angle What is a Triangle?
30 60 90 Triangles
30 60 90 triangle rules
30 60 90 triangle rules-The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SATTriangle30 60 90 This printable triangle has angles of 30, 60, and 90 degrees at its vertices Please make sure to print at 100% or actual size so the rulers will stay true to size



The 30 60 90 Triangle Topics In Trigonometry
General triangle rule () Post by tgf » Sun Nov 29, 09 1051 am Hi, if a right triangle has one angle equal to 30 (or 60) you KNOW the other angle has to be 60 (or 30) and thus the longest side is 2 times the shortest sideWhat is a Triangle?Right triangles are one particular group of triangles and one specific kind of right triangle is a right triangle As the name suggests, the three angles in the triangle are 30, 60, and
Using the triangle to find sine and cosine Before we can find the sine and cosine, we need to build our degrees triangle Start with an equilateral triangle with a side length of 4 like the one you see belowRight Triangle Calculator Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles , the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesWatch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VI
The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SATUsing the pythagorean theorem – As a right angle triangle, the length of the sides of a 45 45 90And then we see that we're dealing with a couple of triangles This one is 30, 90, so this other side right over here needs to be 60 degrees This triangle right over here, you have 30, you have 90, so this one has to be 60 degrees They have to add up to 180, triangle



How To Work With 30 60 90 Degree Triangles Education Is Around



30 60 90 Triangles
30 60 90 Right Triangle Calculator Short Side a Input one number of input area Long Side b Hypotenuse c Area Perimeter Input one number then click "calculate" button!To explore the truth of this rule, try Math Warehouse's interactive triangle, which allows you to drag around the different sides of a triangle and explore the relationship between the angles and sidesNo matter how you position the three sides of the triangle, the total degrees of all interior angles (the three angles inside the triangle) is always 180°Triangle30 60 90 This printable triangle has angles of 30, 60, and 90 degrees at its vertices Please make sure to print at 100% or actual size so the rulers will stay true to size



30 60 90 Triangle Theorem Ratio Formula Video


Solve A 30 60 90 Triangle With Gradea
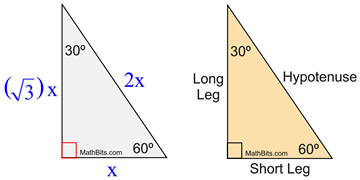
A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 What is the formula for a 45 45 90 Triangle?30° 60° 90° Triangle A triangle where the angles are 30°, 60°, and 90° Try this In the figure below, drag the orange dots on each vertex to reshape the triangle Note how the angles remain the same, and it maintains the same proportions between its sidesHow To Work With degree Triangles 30 60 90 Triangle If you've had any experience with geometry, you probably know


Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education
The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to useSpecial right triangles 30 60 90 Special right triangle 30° 60° 90° is one of the most popular right triangles Its properties are so special because it's half of the equilateral triangle If you want to read more about that special shape, check our calculator dedicated to the 30° 60° 90° trianglePrintable stepbystep instructions for drawing a triangle with compass and straightedge or ruler Math Open Reference Home Contact About Subject Index Constructing a triangle This is the stepbystep, printable version If you PRINT this page, any ads will not be printed


A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education



30 60 90 Right Triangles Ck 12 Foundation
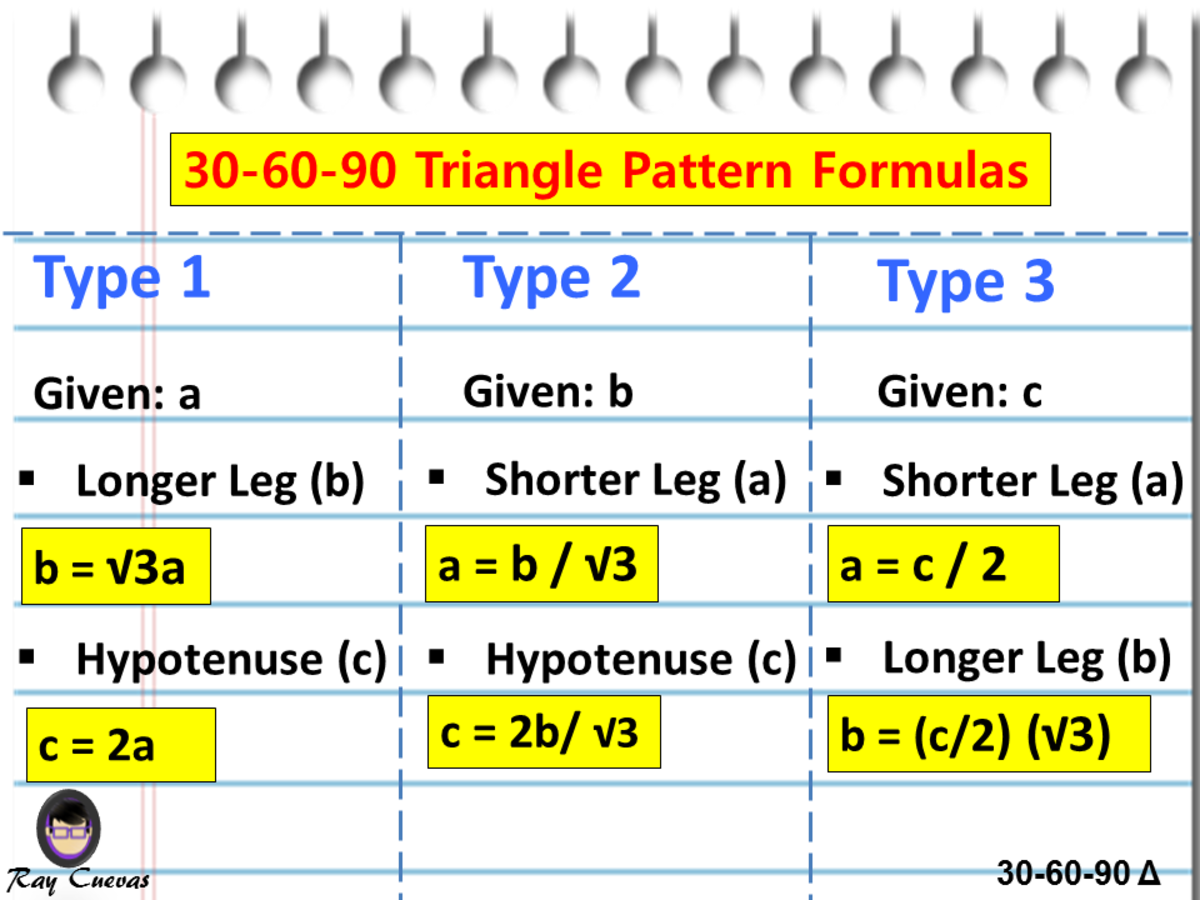
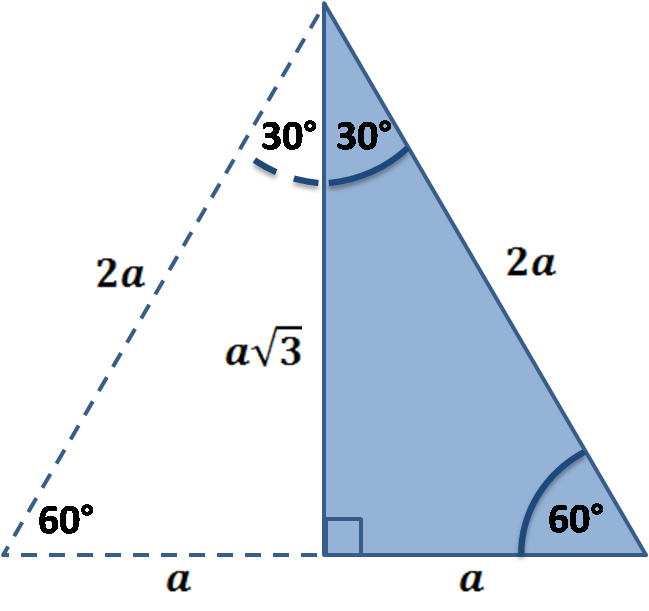
A/c = sin (30°) = 1/2 so c = 2a b/c = sin (60°) = √3/2 so b = c√3/2 = a√3 Also, if you know two sides of the triangle, you can find the third one from the Pythagorean theorem However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle givenA 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊It is a triangle where the angles are always 30, 60 and 90 As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles Example of 30 – 60 90 rule



Special Right Triangles Review Article Khan Academy


Why In A 30 60 90 Triangle Is The The Side Opposite 60 Degrees X Sqrt 3 Quora
The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SATTHE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that belowA triangle is a unique right triangle It is an equilateral triangle divided in two on its center down the middle, along with its altitude A degree triangle has angle measures of 30°, 60°, and 90° A triangle is a particular right triangle because it has length values consistent and in primary ratio



30 60 90 Triangle Theorem Ratio Formula Video


A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education
30° 60° 90° Triangle A triangle where the angles are 30°, 60°, and 90° Try this In the figure below, drag the orange dots on each vertex to reshape the triangle Note how the angles remain the same, and it maintains the same proportions between its sidesUsing the triangle to find sine and cosine Before we can find the sine and cosine, we need to build our degrees triangle Start with an equilateral triangle with a side length of 4 like the one you see below Then, from one vertex, draw the line that is perpendicular to the side opposite the vertexSo if this is 30, this is 90, and let's say that this is x x plus 30 plus 90 is equal to 180, because the angles in a triangle add up to 180 We know that x is equal to 60 Right?



30 60 90 Triangles Hd Youtube



30 60 90 Triangle Theorem Ratio Formula Video
A triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middleWest Coast Paracord 9 Piece Mathematics Tool Set – Straight Ruler, 30/60/90 Triangle Ruler, 45/90 Triangle Ruler, 180 Degree Protractor and More!The Pythagorean theorem (the sum of the square of the sides of a right triangle equal the hypotenus With that comes the famous 3, 4, 5 right triangle (squares are 9 16 = 25) and then a 3060 right triangle, where if the non 90 degree angles are 30 and 60 degrees, the shortest side is 1/2 the hypotenus



The Complete Guide To The 30 60 90 Triangle



30 60 90 Triangle Explanation Examples
Clear/Black Includes Sturdy Storage Case $1049 $ 10 49Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle Solution As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another


Precalculus Notes Trig 3



The 30 60 90 Triangle Topics In Trigonometry
The other triangle is named a triangle, where the angles in the triangle are 30 degrees, 60 degrees, and 90 degrees Common examples for the lengths of the sides are shown for each below The Triangle Here we check the above values using the Pythagorean theoremAlthough all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesProperties of a Right Triangle A special kind of triangle A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1\(\sqrt{3}\)2



30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
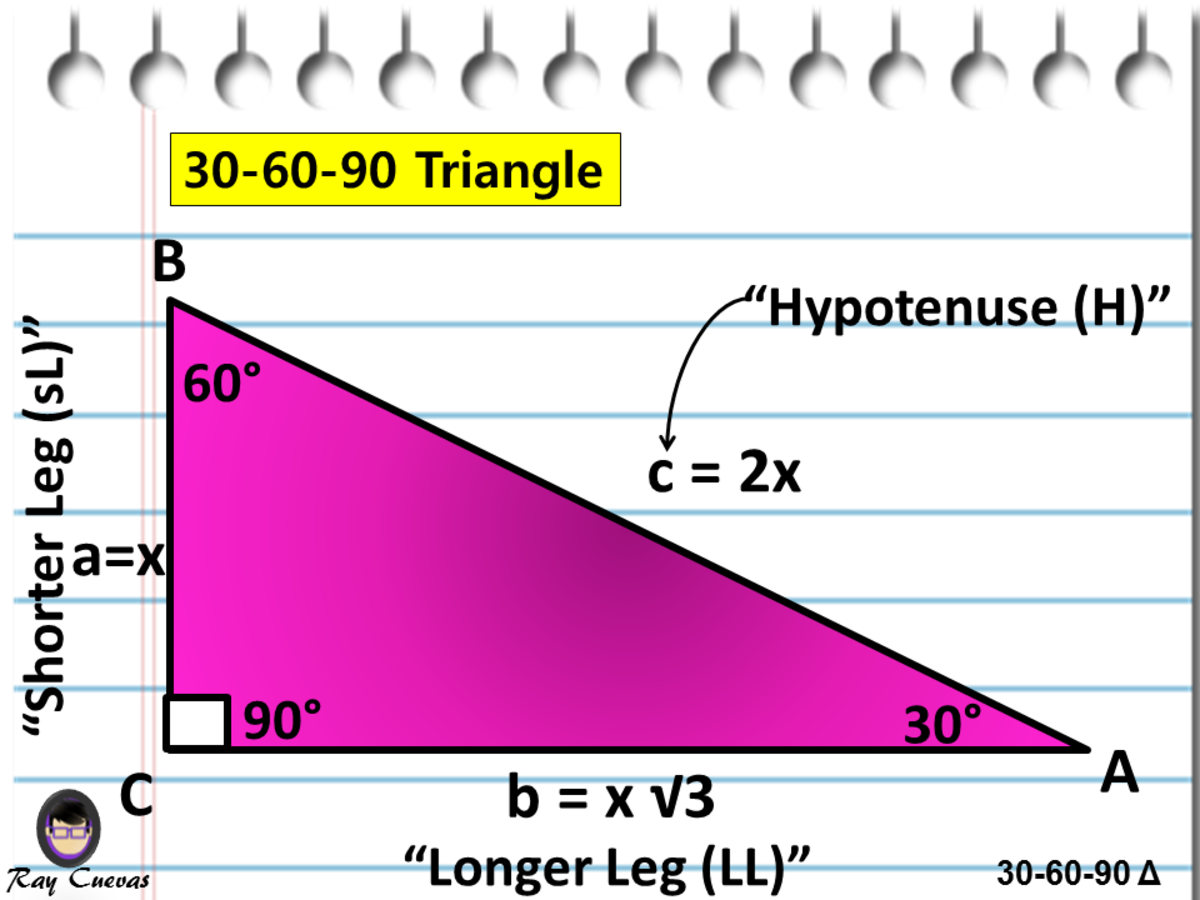
In any triangle, you see the following The shortest leg is across from the 30degree angle, the length of the hypotenuse is always double the length of the shortest leg, you can find the long leg by multiplying the short leg by the square root of 3A triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sidesWest Coast Paracord 9 Piece Mathematics Tool Set – Straight Ruler, 30/60/90 Triangle Ruler, 45/90 Triangle Ruler, 180 Degree Protractor and More!



30 60 90 Triangle Theorem Proof Don T Memorise Youtube
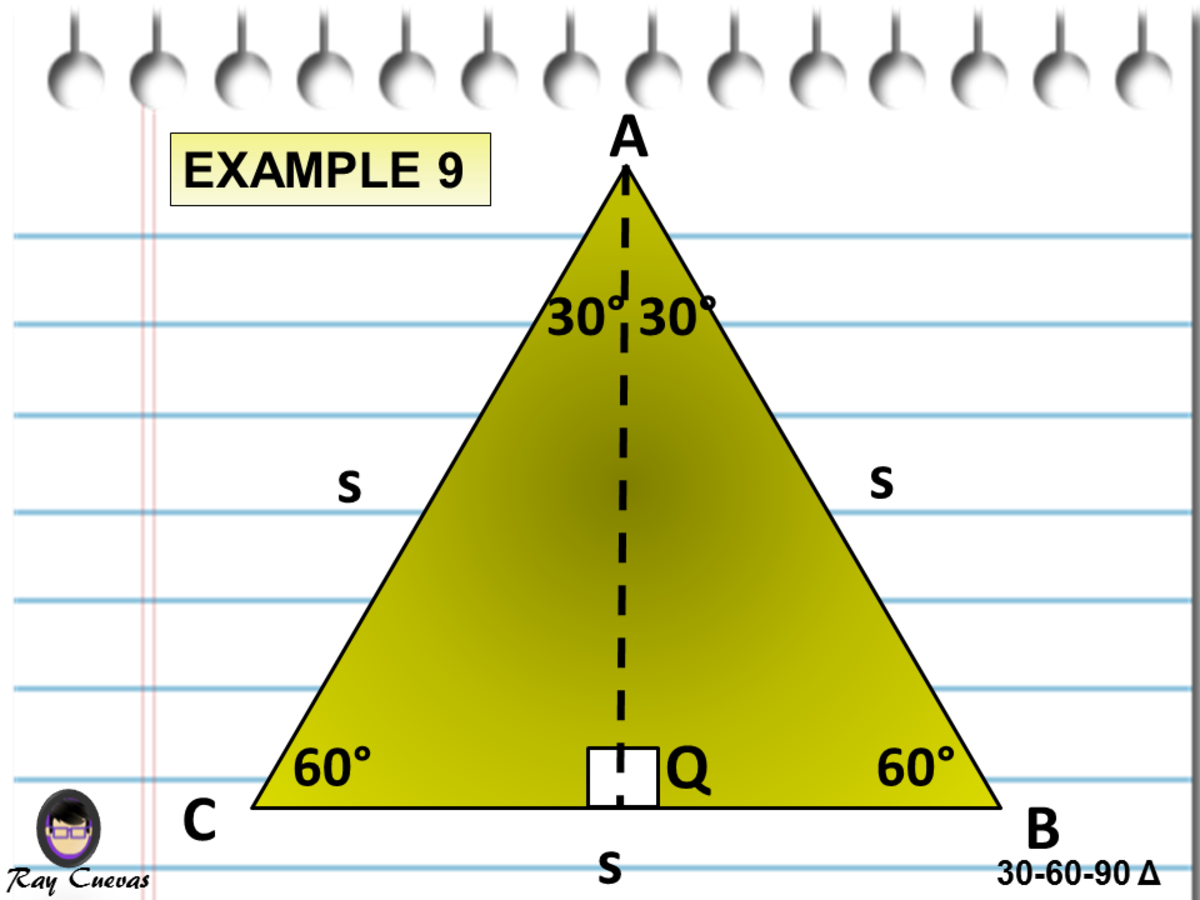


A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherA triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middleA triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education



Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
Triangle Practice Name_____ ID 1 Date_____ Period____ ©v j2o0c1x5w UKVuVt_at iSGoMfttwPaHrGex rLpLeCkQ l ^AullN Zr\iSgqhotksV vrOeXsWesrWvKe`d\1Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60° 6) m n63A triangle is a right triangle whose internal angles are 30, 60 and 90 degrees The three sides of a triangle have the following characteristics All three sides have different lengths The shorter leg, b, is half the length of the hypotenuse, c That is, b=c/2 The longer leg's length, a, is the shorter leg times 3Thatis, a=bAngles 30, 60, 90, 1 Theorems and Problems Table of Content 1 Geometry Problem 1433 Tangent Circles, Diameter, Perpendicular, Midpoint, Measurement, Poster
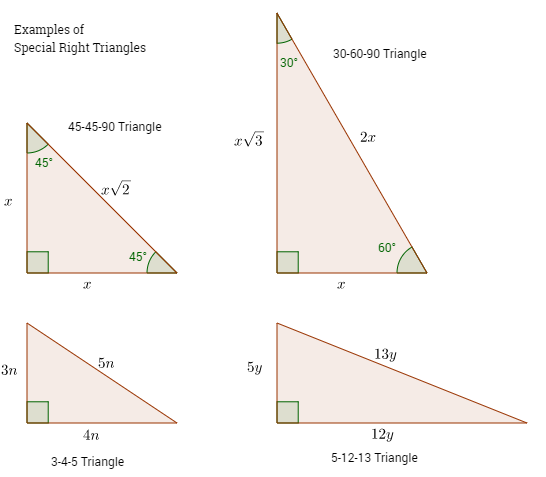


Special Right Triangles Solutions Examples Videos



30 60 90 Triangles Spock S Guide To Math 4
Triangle Practice Name_____ ID 1 Date_____ Period____ ©v j2o0c1x5w UKVuVt_at iSGoMfttwPaHrGex rLpLeCkQ l ^AullN Zr\iSgqhotksV vrOeXsWesrWvKe`d\1Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60° 6) m n63A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of threeSo this angle is 60 And this is why it's called a triangle because that's the names of the three angles in the triangle



30 60 90 Triangle Theorem Ratio Formula Video



Special Right Triangles
Tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees)How To Work With degree Triangles 30 60 90 Triangle If you've had any experience with geometry, you probably knowA 30 60 90 triangle rule can be applied on a rightangled triangle with angles \(30{^\circ}\), \(60{^\circ}\), and \(90{^\circ}\), When at least one of the sides is given, the others can be calculated using the triangle rule Let's see how we can solve a 30 60 90 triangle using the rule in our next section
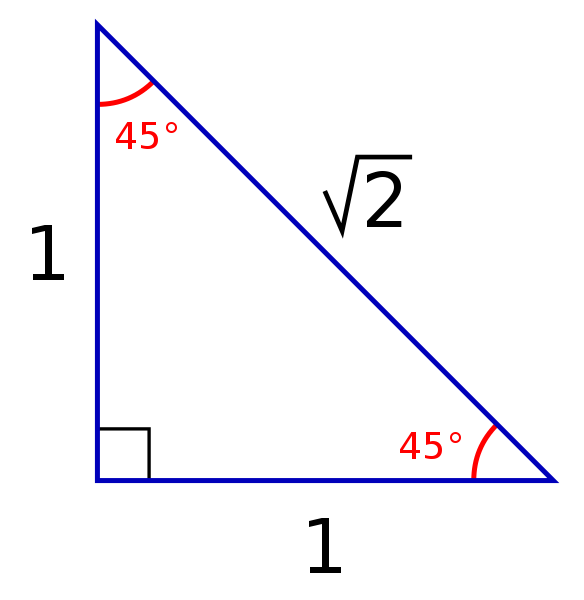


30 60 90 Triangle Formulas Rules And Sides Science Trends



30 60 90 Right Triangle Side Ratios Expii
Clear/Black Includes Sturdy Storage Case $1049 $ 10 49About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators



Agenda 2 27 1 Bell Work 2 Ip Check 3 Outcomes 4 Pythagorean Proof 2 From 9 2 Notes 5 Special Right Triangles A B Ppt Download


The Easy Guide To The 30 60 90 Triangle



Special Rules For 30 60 90 Triangles Youtube



A Quick Guide To The 30 60 90 Degree Triangle Dummies
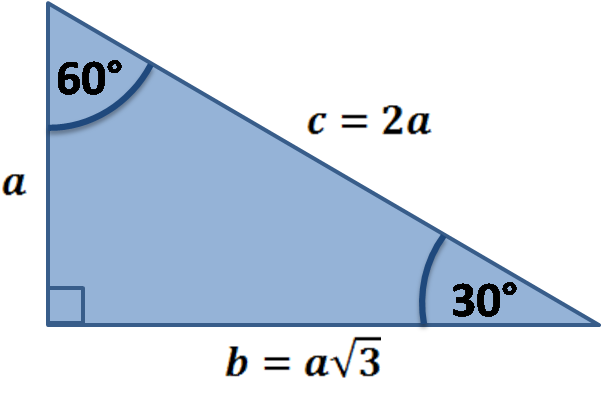


30 60 90 Triangle Calculator Formula Rules



Special Right Triangles Fully Explained W 19 Examples


Special Right Triangles Proof


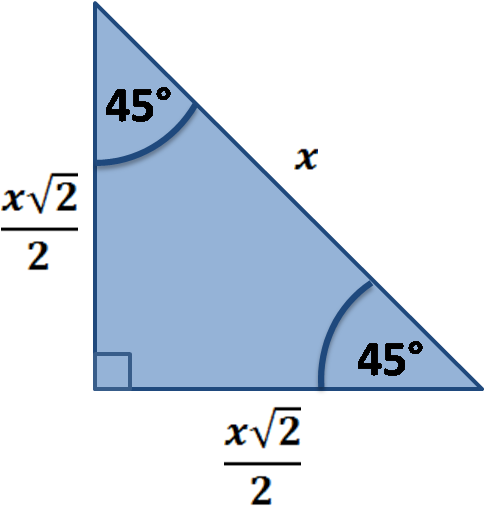
45 45 90 And 30 60 90 Triangles Zona Land Education
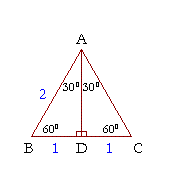


30 60 90 Right Triangle Side Ratios Expii
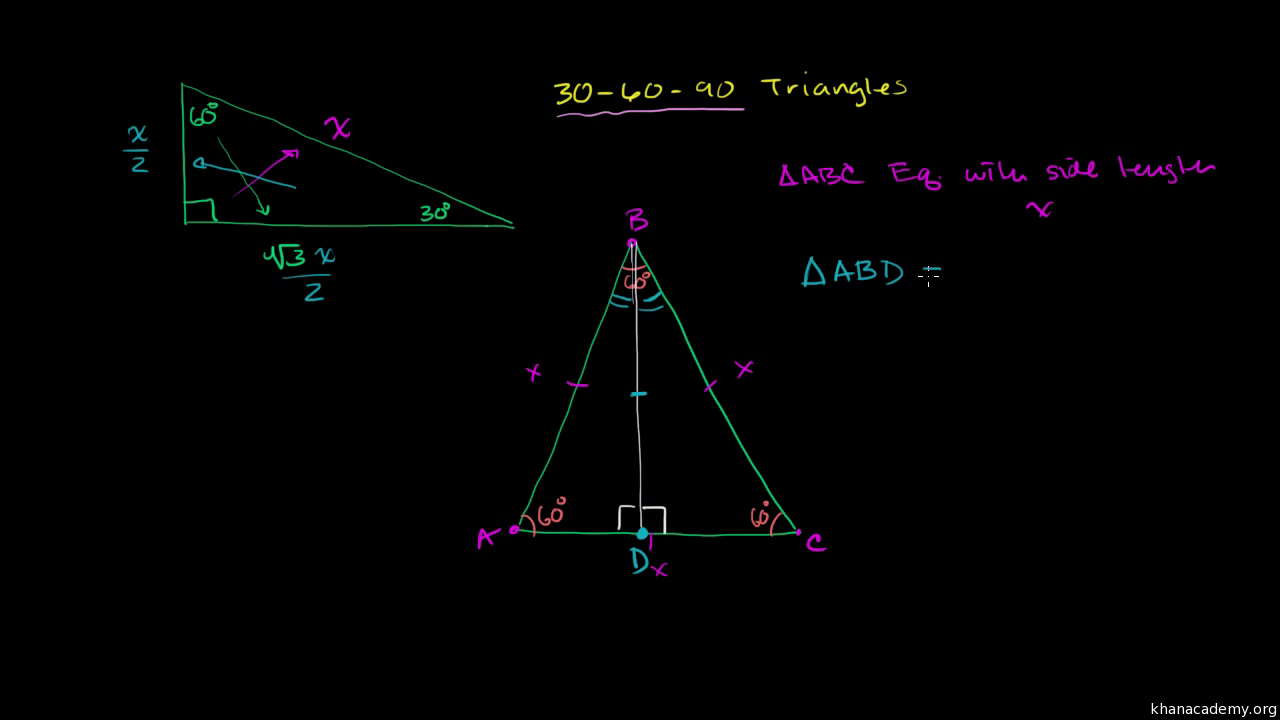


Special Right Triangles Proof Part 1 Video Khan Academy



30 60 90 Triangle Explanation Examples


Right Triangles Gmat Free



30 60 90 Triangles



30 60 90 Triangle Calculator Formula Rules



30 60 90 Triangle Sides Examples Angles Full Lesson
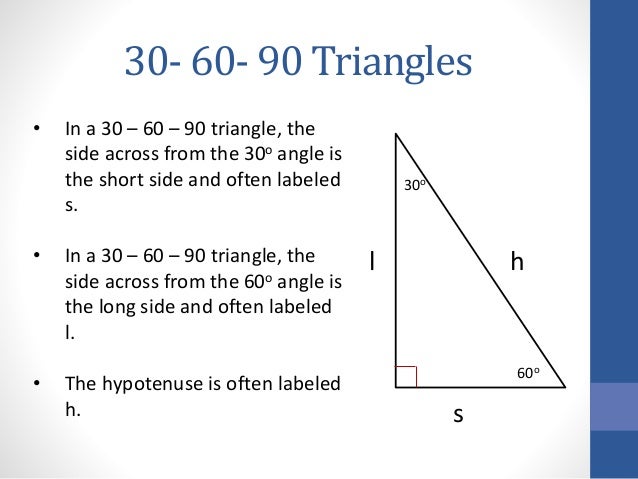


30 60 90 Triangles


The Easy Guide To The 30 60 90 Triangle
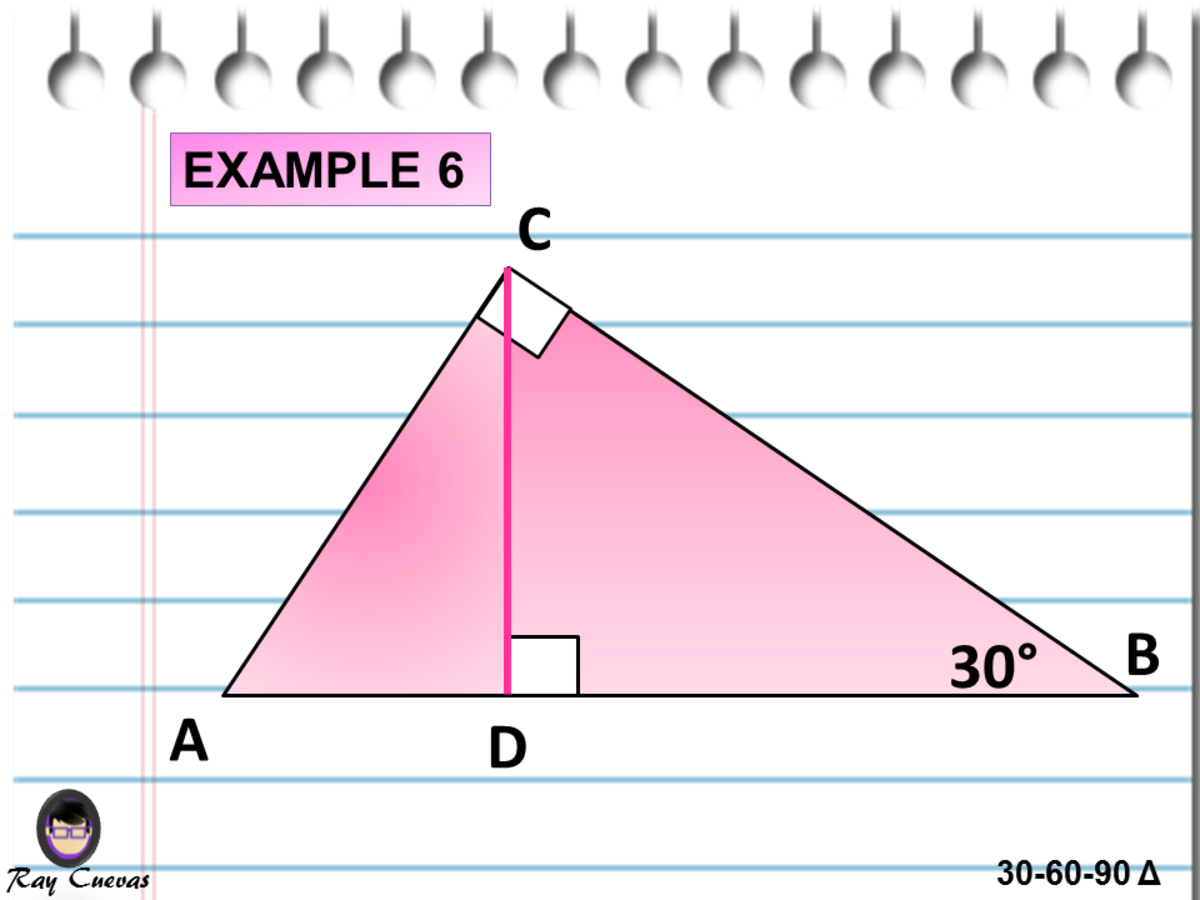


A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education


Special Right Triangles Calculator Formula Rules


Special Right Triangles Calculator Formula Rules



Special Right Triangles Interactive Notebook Page Teaching Geometry Math Methods Studying Math


Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube


30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
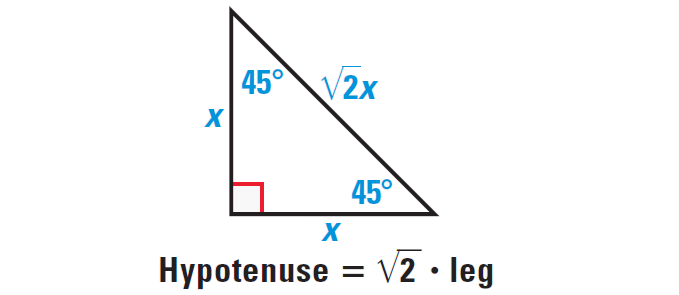


Special Right Triangles
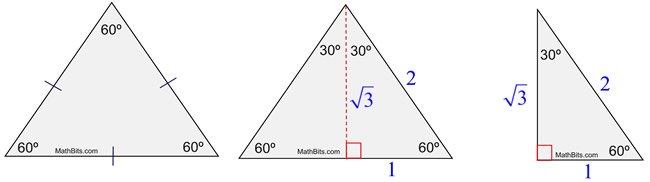


Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



30 60 90 Triangle Theorem Ratio Formula Video



Theorem Of 30 60 90 Triangle In Marathi Marathi Trigonometric Proves And Word Problems Class 10 Unacademy


The Easy Guide To The 30 60 90 Triangle



30 60 90 Special Right Triangle Calculator Inch Calculator



30 60 90 Triangle Theorem Ratio Formula Video
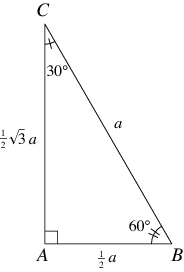


30 60 90 Triangle From Wolfram Mathworld



30 60 90 Triangle Theorem Ratio Formula Video



8 2 Special Right Triangles Ppt Video Online Download



30 60 90 Right Triangles Ck 12 Foundation



Special Right Triangle Wikipedia



30 60 90 Triangles



The Length Of The Hypotenuse Of A 30 60 90 Triangle Is 15 Find The Perimeter Brainly Com



The Complete Guide To The 30 60 90 Triangle
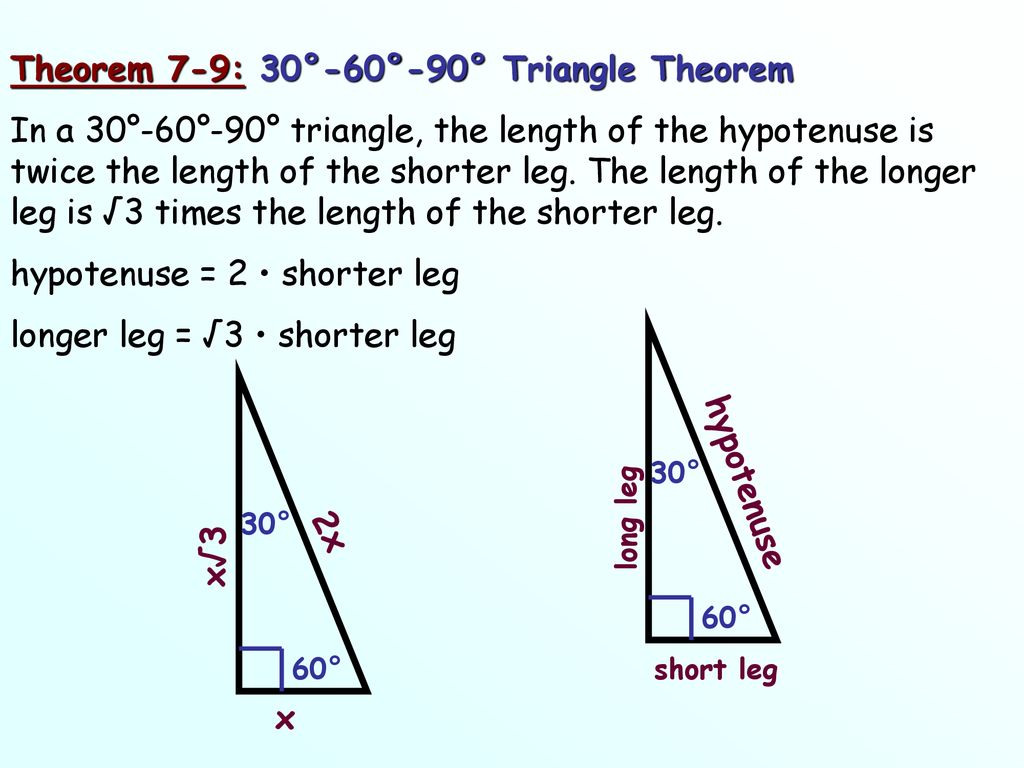


Objective To Use The Properties Of 30 60 90 Triangle Ppt Download


Special Right Triangles
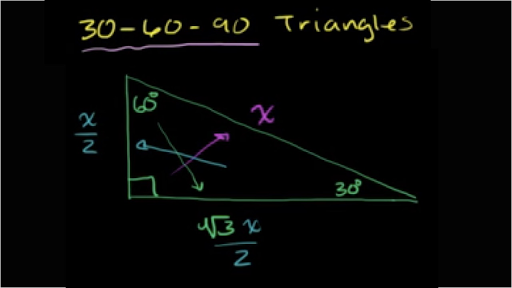


Special Right Triangles Proof Part 1 Video Khan Academy
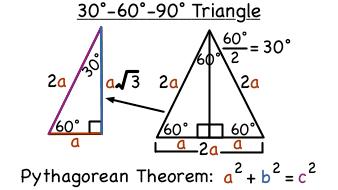


What Is A 30 60 90 Degree Triangle Virtual Nerd
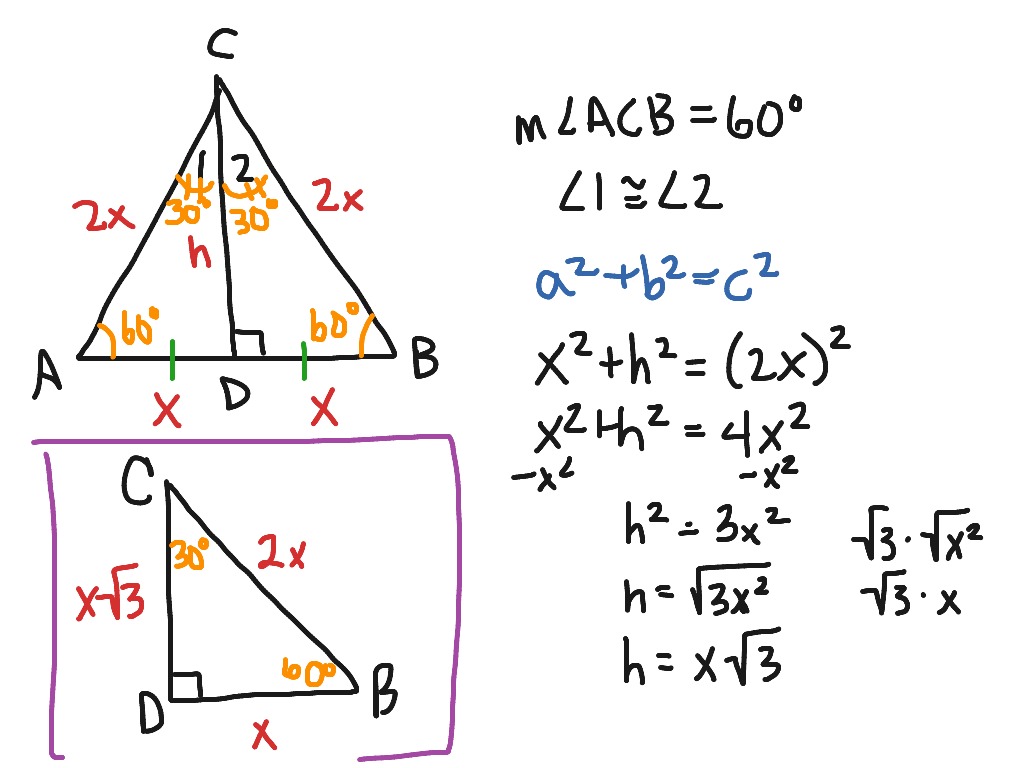


30 60 90 Triangle Math Right Triangles Showme



The 30 60 90 Triangle Topics In Trigonometry


5 5 Special Triangles
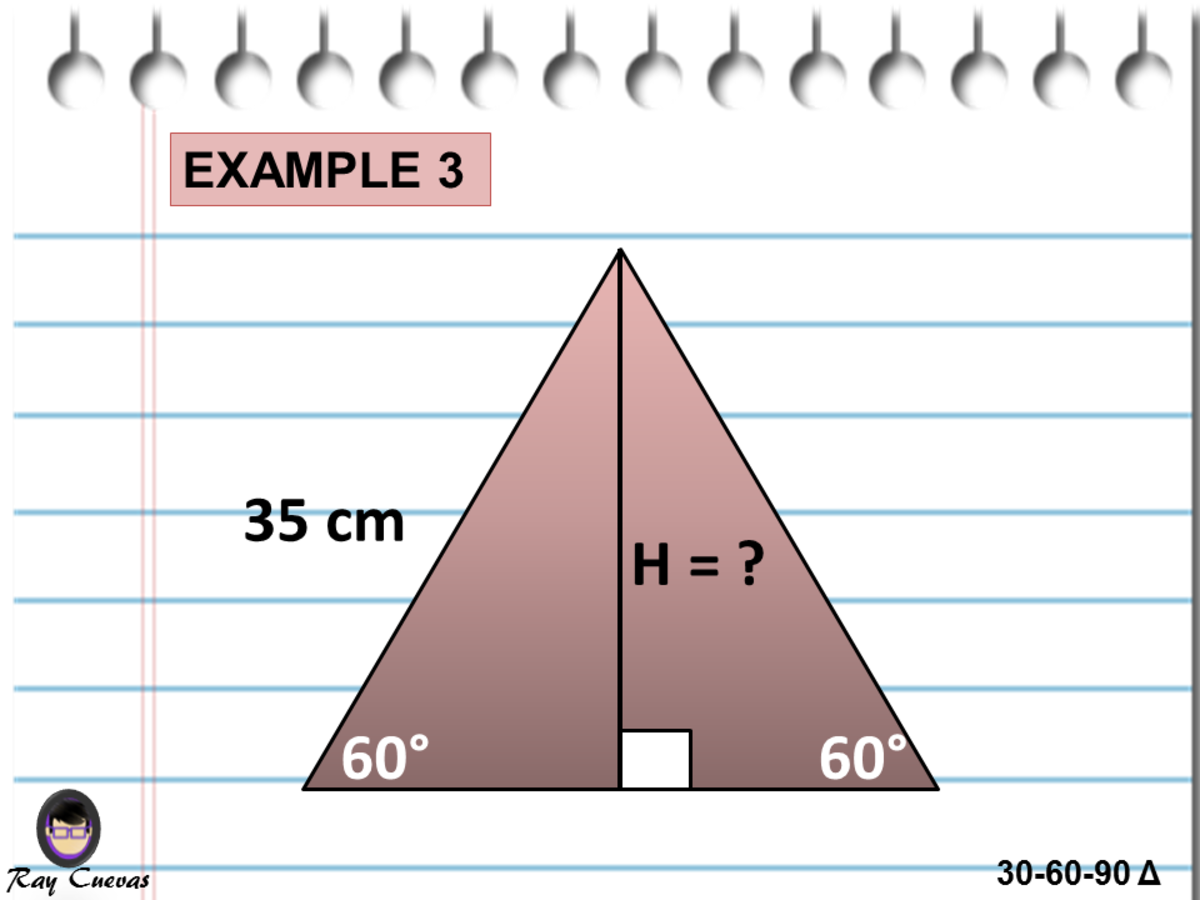


A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education


The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle Calculator Formula Rules


Right Triangles Gmat Free



30 60 90 Right Triangles Read Geometry Ck 12 Foundation


30 60 90 And 45 45 90 Triangle Calculator
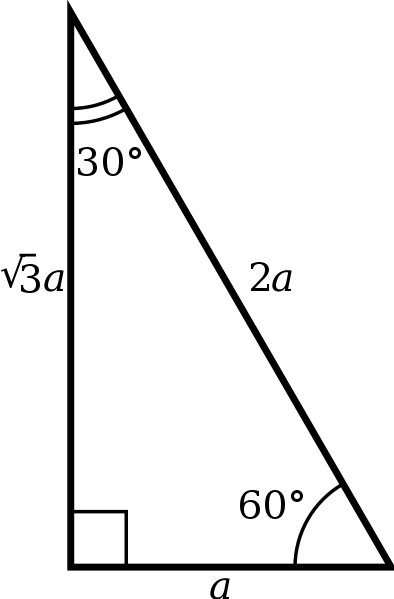


30 60 90 Triangle Formulas Rules And Sides Science Trends
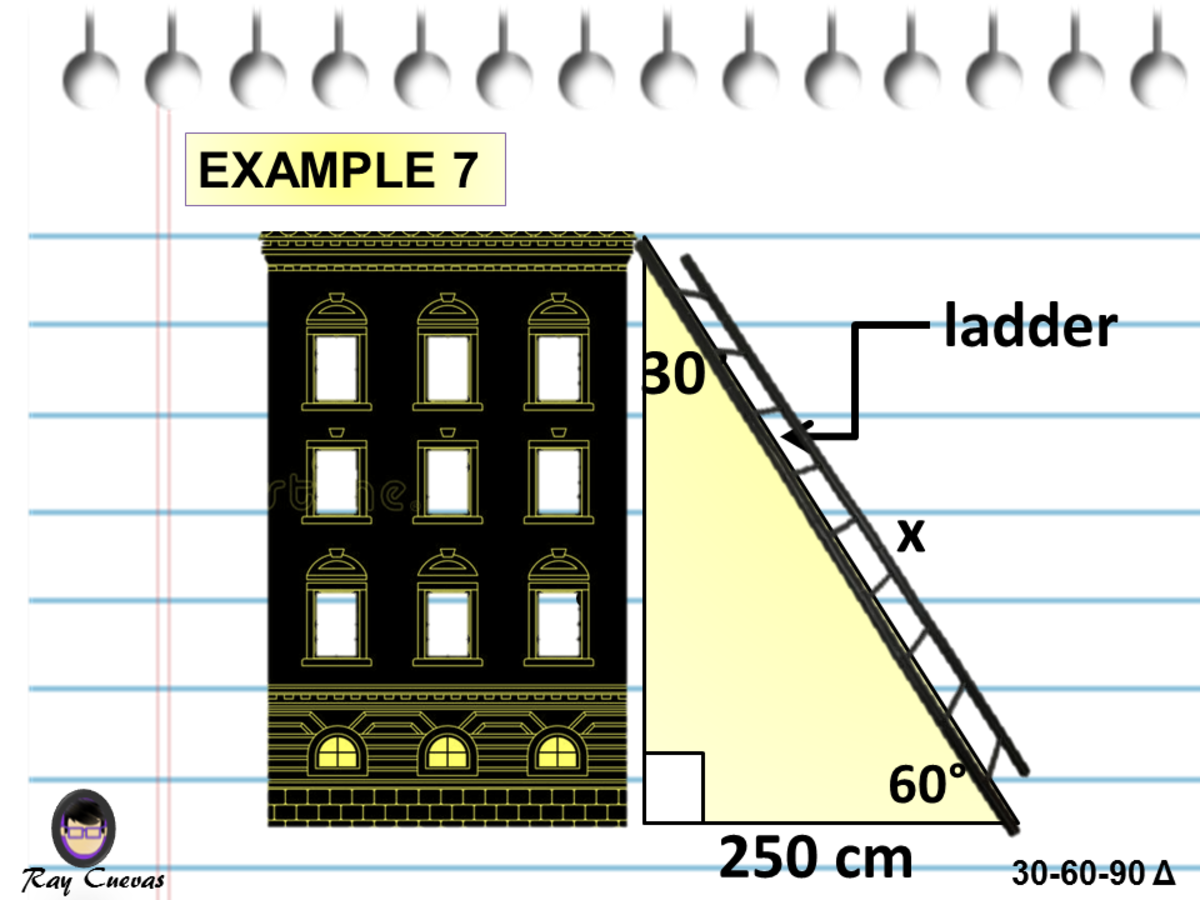


A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education



30 60 90 Triangle Calculator Formula Rules
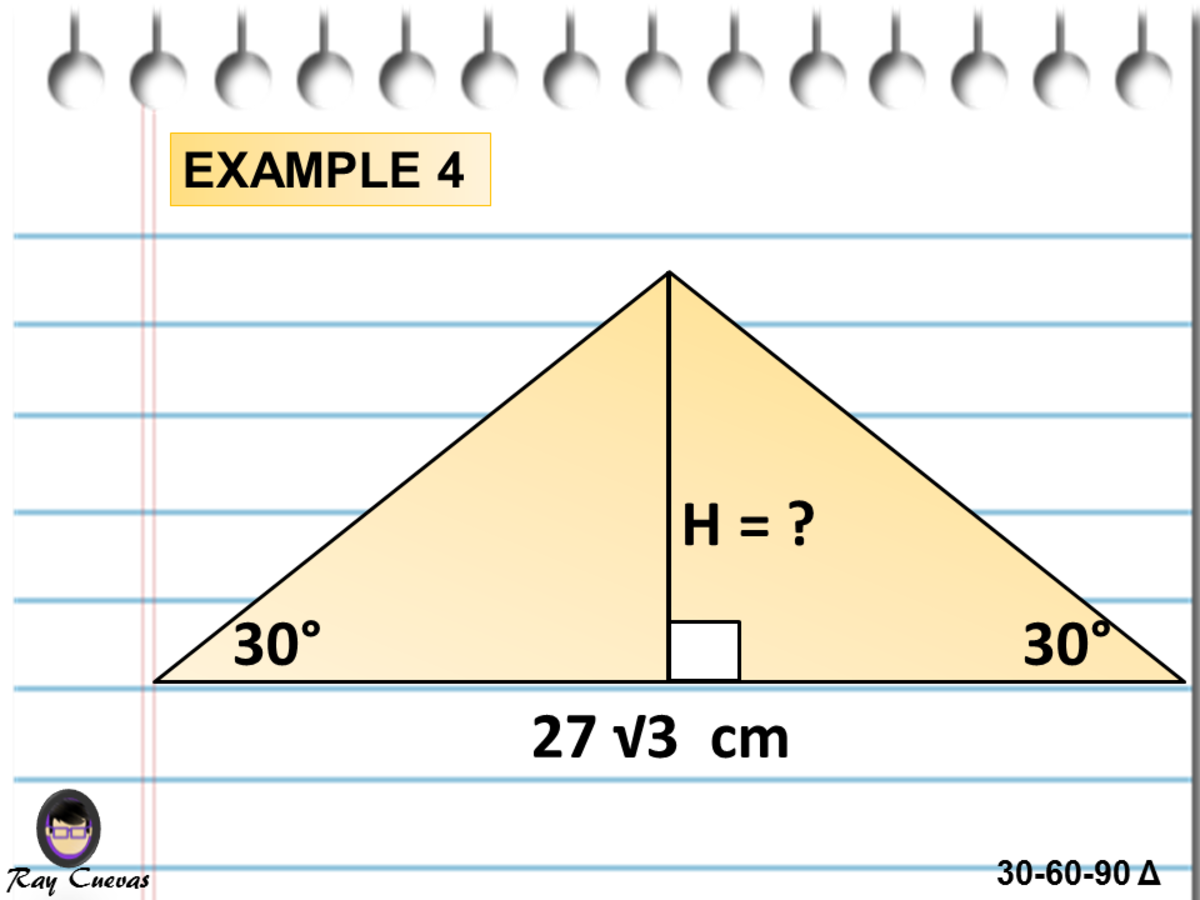


A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education


The Easy Guide To The 30 60 90 Triangle



30 60 90 Right Triangles Free Math Help
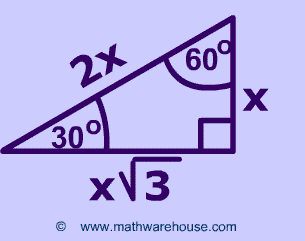


Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



A Quick Guide To The 30 60 90 Degree Triangle Dummies


The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle Formulas Rules And Sides Science Trends



The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet



30 60 90 Triangle Example Problem Video Khan Academy



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation Education
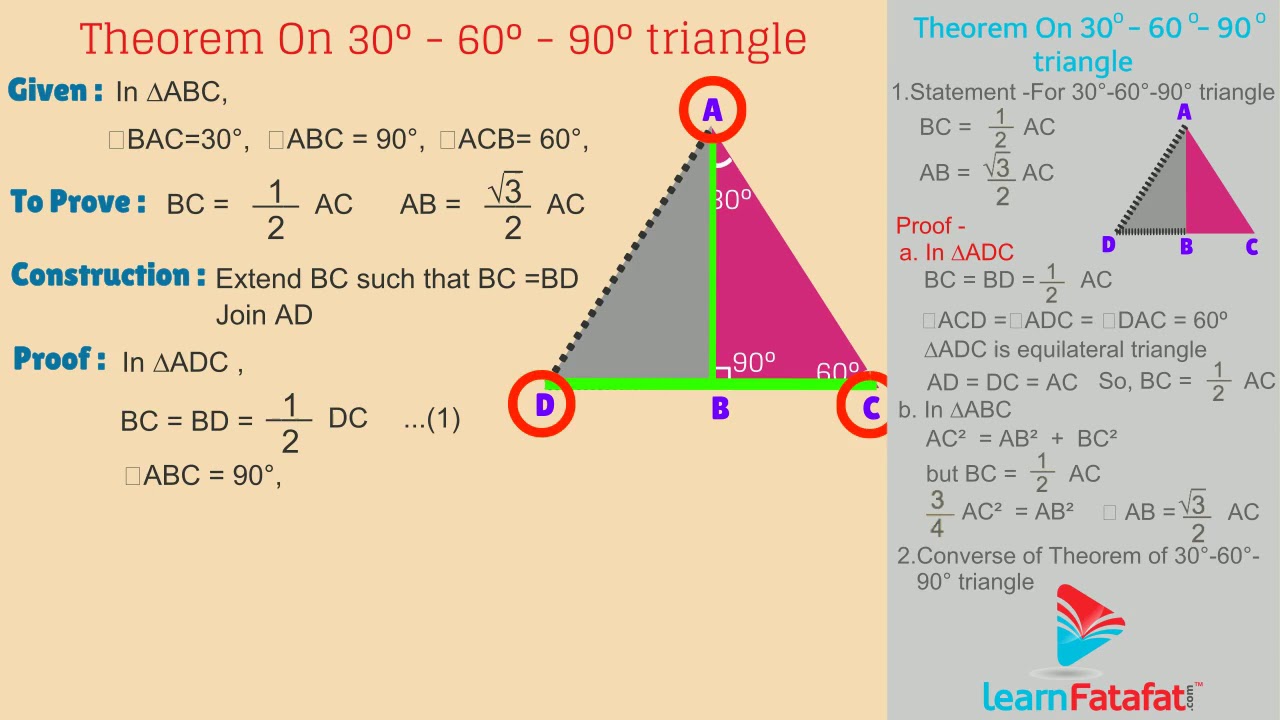


Pythagoras Theorem On 30 60 90 Triangle Youtube


30 60 90 Triangle Calculator Formula Rules



30 60 90 Triangle Theorem Ratio Formula Video


The Easy Guide To The 30 60 90 Triangle



30 60 90 Right Triangles Solutions Examples Videos



30 60 90 Triangle Theorem Ratio Formula Video



0 件のコメント:
コメントを投稿